原文題目
Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

題目摘要

1. 給定一個 m x n 的字母陣列 board 和一個字串 word。如果 word 存在於陣列中則回傳 true ，否則回傳 false。
2. word 須由陣列中四方相鄰的字母組成，四方相鄰即為水平或垂直相鄰的（上下左右）。
3. 同一格中的字母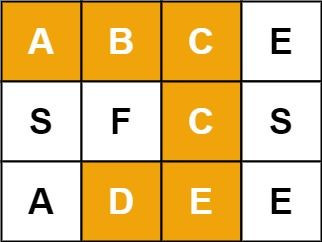不能被重複使用。

Example 1:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2: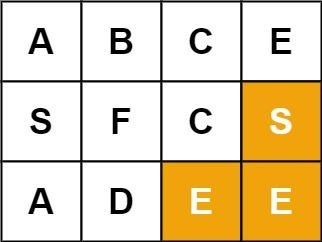

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

解題思路

1. 設定變數與訪問矩陣：
   • 計算矩陣的行數和列數，並使用一個與矩陣相同大小的二維矩陣 visited 來記錄每個格子是否已經被訪問過。
2. 遍歷矩陣：
   • 遍歷矩陣上的每個格子，當遇到與 word 的第一個字母匹配的格子時，啟動深度優先搜尋（DFS）。
3. 深度優先搜尋（DFS）:
   • 定義一個遞迴函數 dfs，它會檢查當前格子是否在邊界內、是否已被訪問過，以及該格子的字母是否與 word 中當前需要匹配的字母相同。
   • 如果當前格子符合條件，將其標記為已訪問，並遞迴搜尋四個方向（上、下、左、右）的相鄰格子。
   • 如果任意方向能找到整個字串，則回傳 true。
   • 如果當前路徑不成功（即無法找到完整的字串）則回溯，將該格子標記為未訪問，並繼續嘗試其他路徑。
4. 回傳結果：
   • 如果整個矩陣遍歷後仍未找到匹配的字串，則回傳 false。

程式碼

class Solution {
    public boolean exist(char[][] board, String word) {
        int row = board.length; //設立棋盤列數
        int column = board[0].length; //設立棋盤行數
        int visited[][] = new int[row][column]; //設立二維矩陣來記錄每個格子的訪問狀況

        //遍歷棋盤的所有格子
        for (int i = 0; i < row; i++){
            for (int j = 0; j < column; j++){
                //如果找到匹配word的第一個字母，則開始深度優先搜索
                if (word.charAt(0) == board[i][j]){
                    if (dfs(board, word, visited, i, j, 0)){
                        return true; //如果能找到整個單詞，則回傳true
                    }
                }
            }
        }
        
        return false; //如果遍歷完整個棋盤後仍未找到，則回傳false
    }

    private boolean dfs(char[][] board, String word, int visited[][], int r, int c, int index){
        //如果已經找到整個單詞，則回傳true
        if (index == word.length()){
            return true;
        }  

        //如果超出邊界、已經訪問過或當前格子不匹配字母，則回傳false
        if(r < 0 || c < 0 || r == board.length || c == board[0].length || visited[r][c] == 1 || word.charAt(index) != board[r][c]){
            return false;            
        }

        visited[r][c] = 1; //標記當前格子為已訪問

        //深度優先搜索上下左右四個方向
        if (dfs(board, word, visited, r+1, c,index+1) ||
            dfs(board, word, visited, r,c+1, index+1) || 
            dfs(board, word, visited, r-1,c, index+1) || 
            dfs(board, word, visited, r,c-1, index+1)){
            return true; //如果任意方向能找到整個單詞，則回傳 true
        }

        visited[r][c] = 0; //回溯，將當前格子標記為未訪問
        return false; //如果無法找到整個單詞，則回傳 false
    }
}

結論
這題我用了深度優先搜尋（DFS）來查找字母是否按順序組成給定字串。DFS 對每個可能的起點進行遞迴搜索，並且在每一步都檢查當前字母是否符合要求。當某條路徑無法匹配，就回到上一步來嘗試其他可能的路徑。所以 DFS 其實也是一種回溯法，它通過逐步探索可能的解，並在失敗時回退到上一步，繼續探索其他路徑。這樣的搜索策略使得解決此問題具備靈活性，能有效地處理不同的起點和字母排列。